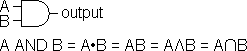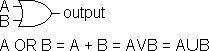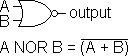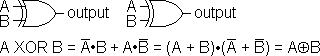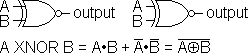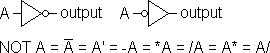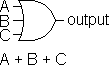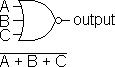| AND Gate |
|
NAND Gate |
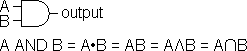 |
 |
Output is TRUE only if both inputs are TRUE. |
Output is FALSE only if both inputs are TRUE. |
| A B | output |
|
| F F | F |
| F T | F |
| T F | F |
| T T | T |
|
| A B | output |
|
| F F | T |
| F T | T |
| T F | T |
| T T | F |
|
|
| OR Gate |
NOR Gate |
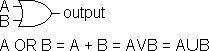 |
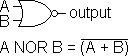 |
Output is TRUE if either input (or both) is TRUE. |
Output is FALSE if either input (or both) is TRUE. |
| A B | output |
|
| F F | F |
| F T | T |
| T F | T |
| T T | T |
|
| A B | output |
|
| F F | T |
| F T | F |
| T F | F |
| T T | F |
|
|
| EXCLUSIVE OR (XOR) Gate |
EXCLUSIVE NOR (XNOR) Gate
(or Equality Gate) |
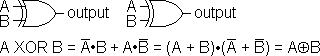 |
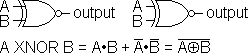 |
Output is TRUE if either (but not both) input is TRUE. |
Output is FALSE if either (but not both) input is TRUE. |
| A B | output |
|
| F F | F |
| F T | T |
| T F | T |
| T T | F |
|
| A B | output |
|
| F F | T |
| F T | F |
| T F | F |
| T T | T |
|
|
Inverter
(or NOT Function or Compliment Function) |
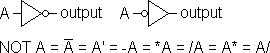 |
|
| AND Gate |
|
NAND Gate |
 |
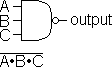 |
Output is TRUE only if all inputs are TRUE. |
Output is FALSE only if all inputs are TRUE. |
| A B C | output |
|
| F F F | F |
| F F T | F |
| F T F | F |
| F T T | F |
| T F F | F |
| T F T | F |
| T T F | F |
| T T T | T |
|
| A B C | output |
|
| F F F | T |
| F F T | T |
| F T F | T |
| F T T | T |
| T F F | T |
| T F T | T |
| T T F | T |
| T T T | F |
|
|
| OR Gate |
NOR Gate |
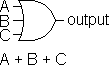 |
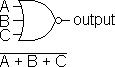 |
Output is TRUE if any input (or all) is TRUE. |
Output is FALSE if any input (or all) is TRUE. |
| A B C | output |
|
| F F F | F |
| F F T | T |
| F T F | T |
| F T T | T |
| T F F | T |
| T F T | T |
| T T F | T |
| T T T | T |
|
| A B C | output |
|
| F F F | T |
| F F T | F |
| F T F | F |
| F T T | F |
| T F F | F |
| T F T | F |
| T T F | F |
| T T T | F |
|
| IF N AND 1 THEN |
|
Tests if a number is odd (has its 1 bit set) |
|
| N + N AND -2 |
Always gives the even number of a pair, so if you are calculating an offset into a buffer, this always places you at an even-numbered position. |
|
| N = N AND X |
Keeps a variable within a range X.
So N AND 16383 insures that an integer never exceeds 16383. |
|
| N = N AND 127 |
Strips the high bit from characters such as for sending to a serial port. |
|
| N = N OR 128 |
Sets the high bit (in some cases this signals an attribute such as underlining). |
|
| N = N AND 95 |
Resets bit 6 to 0 so ASCII characters are upper case.
Replaces IF (ASCII) CODE N) > 96 THEN N = N - 32. |
|
| N = N OR 32 |
Makes all letters lower case by setting bit 6. |
|
| N = N OR 48 |
Converts the digits 0 to 9 into their printable ASCII codes (sets bits 5 and 6). |
|
| IF X OR Y |
If either X or Y has a nonzero value ... |
|
| X = X XOR 1 |
Sets a flag variable from 1 or -1 to 0 and back.
Replaces IF X THEN X = 0 ELSE X = 1. |
|
| PAGE = PAGE XOR 3 |
XOR can be used jump back and forth between two values, here between video pages 1 and 2.
The value that toggles between has 1's where changes occur and 0 where they don't, for example to switch between
| 3 | | 00000011 |
| and 45 | 00101101 |
| use 46 | 00101110 |
|
|
| T = T + 1 AND 3 |
This can be used to maintain a cycle.
Replaces T = T + 1: IF T = 4 THEN T = 0. |
|
| T = 1 - T |
Toggles between 1 and 0. |